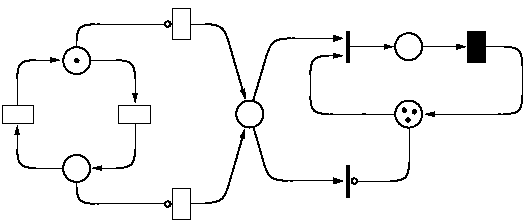
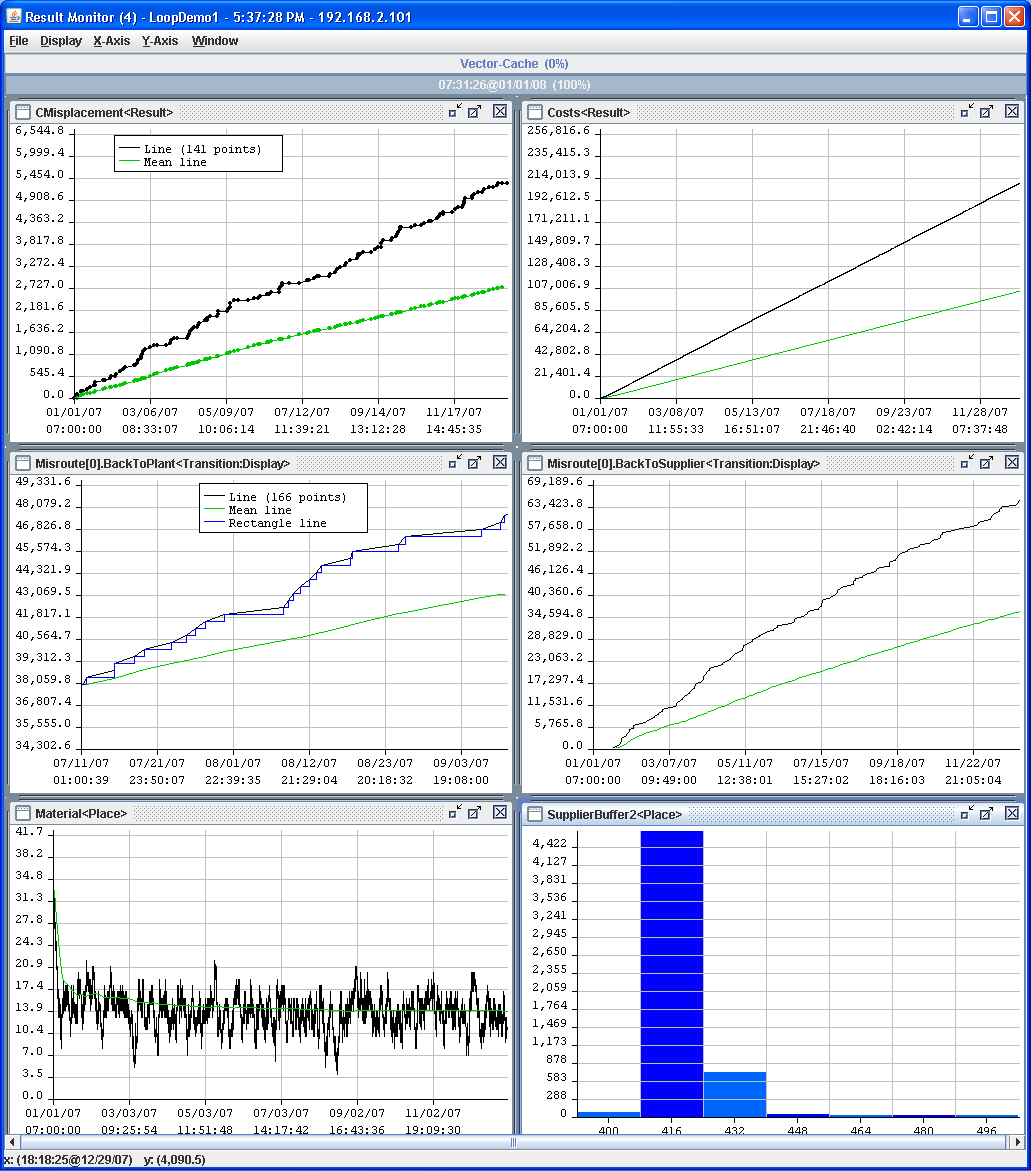
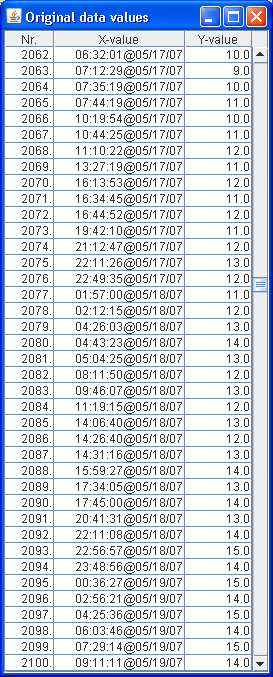
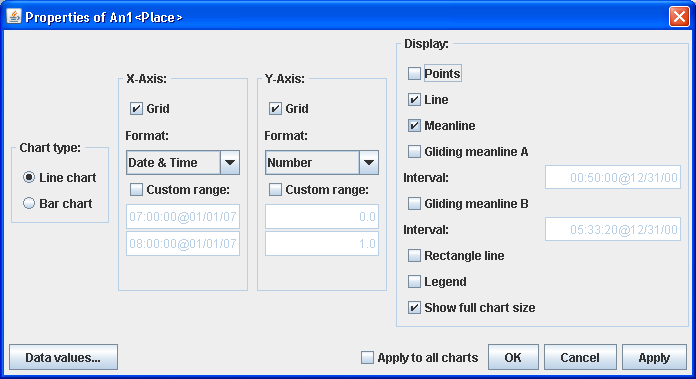
| Function | Description |
| normalize-space() | "Removes all spaces in the beginning and at the end, like the trim() function in Java. |
| Example: normalize-space(' bbb ')= 'bbb' |
| count() | Counts the number of selected elements. |
| name() | Returns the name of the current element. |
| starts-with() | Returns TRUE if the value of the first parameter of the function starts with the value of the second parameter. |
| Example: starts-with(name(), 'first') returns TRUE for the < firstname > element. |
| contains() | Returns TRUE if the first parameter value contains the second parameter value, like the starts-with function. |
| Example: contains(name(), 'name') returns TRUE for all < firstname > and < lastname > elements. |
| string-length() | Returns the length of the given string. |
| Example: string-length('test') return 4. |
|